Wie eine statistische Analyse der Wettquoten zu mehr als 200.000 Fußballspielen und die Hypothese des effizienten Marktes zusammenhängen.
Es gibt viele Mannschaften, die die bevorstehende Fußballweltmeisterschaft in Katar gewinnen können, und niemand kann zu diesem Zeitpunkt wissen, welche von ihnen gewinnen wird. Das Beste, was man tun kann, ist, probabilistische Vorhersagen zu machen. Ich werde hier erklären, wie man die Richtigkeit probabilistischer Vorhersagen überprüfen kann, und werde argumentieren, dass die besten Vorhersagen wohl die sind, die man vom Sportwettenmarkt ableiten kann. Mein Argument basiert auf der Verwendung eines großen Datensatzes von Wettquoten, um die so genannte Markteffizienzhypothese zu testen (https://de.wikipedia.org/wiki/Markteffizienzhypothese).
Der Ausgang eines einzigen Spiels (oder einer einzigen Weltmeisterschaft) reicht nicht aus, um die Vorhersagekraft probabilistischer Vorhersagen zu testen. Nehmen wir an, Sie sagen mit einer Wahrscheinlichkeit von zwei Dritteln voraus, dass Frankreich Australien besiegt, und ich sage mit einer Wahrscheinlichkeit von einem Drittel voraus, dass Frankreich gewinnt. Angenommen, Australien gewinnt. Hatte ich Recht und hatten Sie Unrecht?
Jede Woche gestaltet die „Nationalökonomische Gesellschaft" (NOeG) in Kooperation mit der "Presse" einen Blog-Beitrag zu einem aktuellen ökonomischen Thema. Die NOeG ist ein gemeinnütziger Verein zur Förderung der Wirtschaftswissenschaften.
Beiträge von externen Autoren müssen nicht der Meinung der „Presse"-Redaktion entsprechen.
Es ist im Grunde unmöglich, eine einzelne probabilistische Vorhersage sinnvoll zu testen (es sei denn, Sie sagen Wahrscheinlichkeiten von null oder eins oder sehr nahe daran voraus), aber Sie können eine (große) Menge von Vorhersagen testen. Wettmärkte liefern eine solche Menge von Vorhersagen in Form von Wettquoten, die sich aus Wetten auf die verschiedenen Ergebnisse von Spielen ergeben.
Äquivalent zu den Preisen an der Börse
Wettquoten sind das Äquivalent zu den Preisen an der Börse. Auch sie werden durch Angebot und Nachfrage bestimmt. Da sie sich aber etwas von den Preisen unterscheiden, sollte ich vielleicht kurz erklären, wie sie normalerweise von den Wettanbietern festgelegt werden.
Ein Fußballspiel zwischen den Mannschaften A und B kann mit drei Ergebnissen enden: Mannschaft A gewinnt, Unentschieden oder Mannschaft B gewinnt. Sie können auf jedes dieser drei Ereignisse wetten. Sie können sogar auf noch viel mehr wetten, aber darauf möchte ich hier nicht eingehen. Wenn Sie wetten, erhalten Sie normalerweise Wettquoten. Wenn die Quote q ist, bedeutet das, dass Sie, wenn Sie einen Euro auf diese Wette setzen und gewinnen, q Euro zurückbekommen. Das bedeutet natürlich, dass die Quoten nie kleiner als eins sein können. Mit qA, qD, qB bezeichne ich die Quoten für ein Spiel für die drei Ereignisse: Mannschaft A gewinnt, ein Unentschieden, Mannschaft B gewinnt. Mit bA, bD, bB bezeichne ich die Geldbeträge, die auf diese drei Ereignisse gesetzt werden.
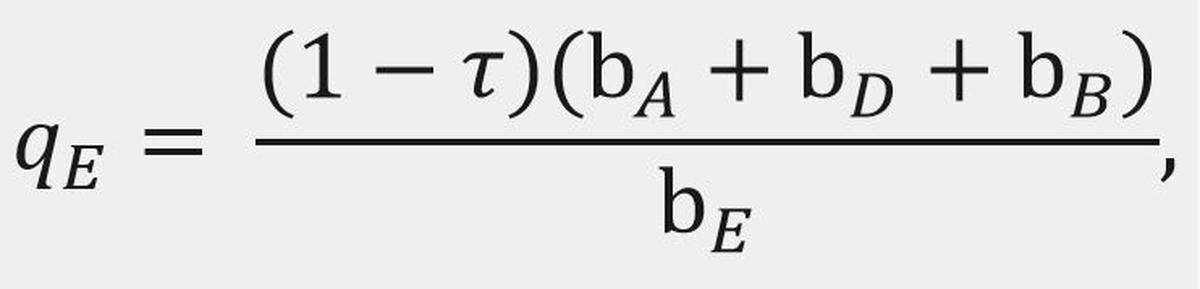
Der Wettanbieter setzt dann die Quoten für jedes Ereignis E aus der Menge {A,D,B} so nahe wie möglich zum Wert wobei 𝜏 der Anteil des Geldes ist, den das Wettunternehmen behält, und oft bei fünf Prozent liegt. Auf diese Weise hat das Wettunternehmen im Grunde kein Risiko und erhält etwa fünf Prozent des gesamten Geldbetrags, der auf die Wetten gesetzt wurde, unabhängig davon, wie das Spiel ausgeht.
Wenn die Wettquote für das Ereignis, dass Mannschaft A gewinnt, q ist, dann ist 1/q die implizite Wahrscheinlichkeit, dass Mannschaft A gewinnt: Wenn 1/q die "wahre" Wahrscheinlichkeit wäre, würden Sie einen Gesamtgewinn aus Ihrer Wette erwarten, der durch q·(1/q) - 1 also genau 0 gegeben ist.) Sie zahlen einen Euro, daher die -1, mit Wahrscheinlichkeit 1/q gewinnen sie q Euro, mit 1-1/q gewinnen sie nichts.) Man könnte sie auch als Break-Even-Wahrscheinlichkeiten bezeichnen. Ein risikoneutraler oder risikoaverser Mensch würde nur dann auf ein Ereignis wetten, wenn er oder sie glaubt, dass die tatsächliche Wahrscheinlichkeit dieses Ereignisses größer ist als diese implizite Break-Even-Wahrscheinlichkeit.
Wenden wir uns nun der statistischen Analyse dieser Wettquoten zu. Ich verwende Wettquoten für mehr als 200.000 professionelle Fußballspiele aus den meisten großen Ligen der Welt zwischen 2006 und 2019 (heruntergeladen von pinnacle.com im April 2019). Ich habe mich hier auf Wetten auf die Siege der Heimmannschaft konzentriert.
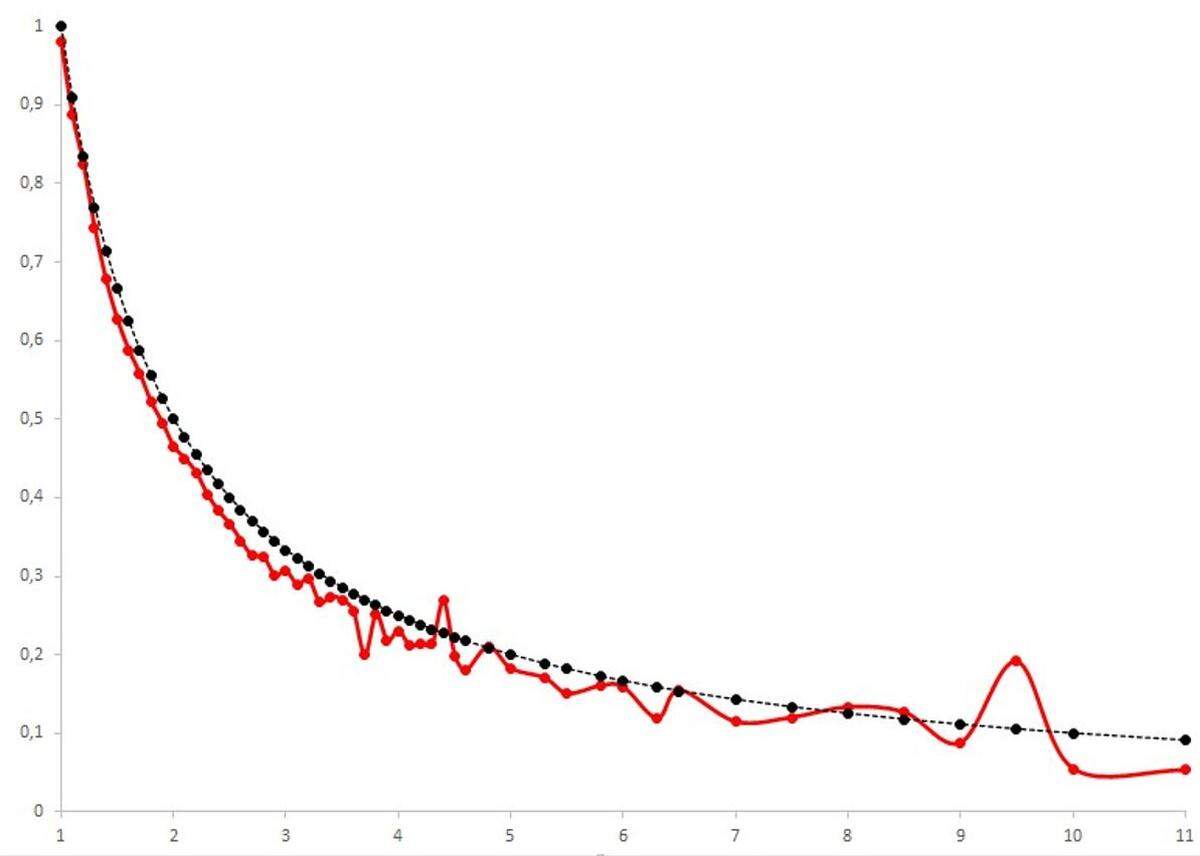
In der obigen Abbildung vergleiche ich die tatsächlich beobachteten Gewinnhäufigkeiten (fette Linie in rot) mit den impliziten Wahrscheinlichkeiten (gestrichelte Linie in schwarz) für alle Quoten zwischen 1 und 11 (auf der x-Achse). Ist es nicht bemerkenswert, wie nahe diesen beiden Kurven beieinander liegen? Um nur zwei Punkte herauszunehmen: Von den 3138 Spielen mit einer Wettquote von 1.2 mit impliziter Break-Even Wahrscheinlichkeit von in etwa 83 Prozent ist die beobachtete Gewinnhäufigkeit 82,3 Prozent. Von den 11045 Spielen mit einer Wettquote von 2,2 und impliziter Break-Even Wahrscheinlichkeit von 45,5 Prozent ist die beobachtete Gewinnhäufigkeit 43,2 Prozent .
Beachten Sie, dass die beiden Kurven aus völlig unterschiedlichen Daten stammen. Die impliziten Wahrscheinlichkeiten werden aus den Wettquoten abgeleitet, die wiederum, wie ich oben erläutert habe, ausschließlich aus dem Wettverhalten auf dem Wettmarkt abgeleitet werden. Die beobachteten Gewinnhäufigkeiten ergeben sich aus der Zählung, wie oft Mannschaften ihre Fußballspiele gewinnen.
Zwei völlig unterschiedliche Dinge. Und doch stimmen sie fast perfekt überein. Man könnte sagen, dass die aus den Wettquoten abgeleiteten impliziten Wahrscheinlichkeiten wirklich gut kalibriert sind: Sie sind großartige Schätzungen der tatsächlichen Gewinnwahrscheinlichkeiten von, in diesem Fall, den Heimmannschaften bei Fußballspielen.
Markteffizienzhypothese
Diese Idee folgt aus der sogenannten Markteffizienzhypothese: die Hypothese, dass in die Marktpreise alle Informationen einfließen, die den Menschen zur Verfügung stehen, und somit die besten Schätzungen für die zugrunde liegenden Wahrscheinlichkeiten liefern.
Zu dem, was ich gerade geschrieben habe, gibt es ein paar Vorbehalte. Betrachtet man die obige Abbildung, so stellt man fest, dass fast alle tatsächlichen Gewinnhäufigkeiten etwas unter den impliziten Gewinnwahrscheinlichkeiten liegen. Das liegt daran, dass das Wettunternehmen seinen Anteil (in der Regel etwa fünf Prozent) beibehält. Das könnte man allerdings leicht anpassen. Das bedeutet auch, dass Sie insgesamt Geld verloren hätten, wenn Sie einen Euro auf jedes einzelne dieser Spiele gesetzt hätten.
Was aber ist mit den wenigen Quoten, bei denen die implizite Wahrscheinlichkeit über der beobachteten Gewinnhäufigkeit liegt? Dies ist bei 6 von 53 Quoten der Fall. Es passiert bei Quoten von 4.4, 4.8, 6.5, 8, 8.5 und 9.5. Bedeutet dies, dass wir in Zukunft auf Spiele mit diesen speziellen Quoten wetten sollten und dabei im Durchschnitt Geld verdienen werden? Steht dies im Widerspruch zur Markteffizienzhypothese?
Das glaube ich nicht. Es gibt im Datensatz nicht so viele Spiele mit diesen Wettquoten. Es sind insgesamt 2292 Spiele. Für die beiden Wettquoten von 4,4 und 9,5, für die die beobachtete Gewinnhäufigkeit deutlicher über den impliziten Break-Even Wahrscheinlichkeit liegt, sind es sogar nur 26 und 94 Spiele. Man kann zeigen, dass, auch wenn die echten Gewinnwahrscheinlichkeiten kleiner oder gleich den impliziten Break-Even Wahrscheinlichkeiten sind, man relativ leicht rein durch Zufall bei ein paar Wettquoten erhöhte beobachtete Gewinnhäufigkeiten bekommen kann. Für die statistisch Interessierten unter Ihnen: Man kann die Nullhypothese, dass alle tatsächlichen Gewinnwahrscheinlichkeiten für alle Wettquoten kleiner oder gleich den jeweiligen impliziten Break-Even Wahrscheinlichkeiten sind, mit den gegebenen Daten nicht verwerfen (p-Wert von 0,189).
Es bleibt eine Glaubensfrage
Wir können also die aus der Markteffizienzhypothese abgeleitete Nullhypothese, dass die Wettquoten gut kalibriert sind, nicht zurückweisen. Heißt das, dass man nicht potenziell bessere probabilistische Vorhersagen machen könnte? Bedeutet das, dass die Hypothese des effizienten Marktes wahr ist? Nein. Dies ist nur ein möglicher Test der Markteffizienzhypothese, die ja nicht nur besagt, dass die impliziten Wahrscheinlichkeiten gut kalibriert sein sollten, sondern auch, dass sie alle Informationen enthalten, die über die Spiele in der Welt verfügbar sind. In gewisser Weise wissen wir, dass dies nicht der Fall ist. Gelegentlich gibt es Spiele, die manipuliert sind. Das bedeutet, dass es einige Leute gibt, die wissen, wie diese Spiele ausgehen werden, und diese Information spiegelt sich oft nicht in den Wettquoten wider. Aber im Großen und Ganzen, und das bleibt ein bisschen eine Glaubensfrage, bin ich der Meinung, dass es schwer ist, genauere probabilistische Vorhersagen über den Ausgang von Fußballspielen zu treffen als die, die sich aus dem Wettmarkt ergeben.
Wer wird die WM also gewinnen? Nach den Wettquoten vom 9. 11. (von oddschecker.com) ist Brasilien mit 23,8 Prozent Wahrscheinlichkeit Favorit (Wettquote 4,2). Darauf folgen Argentinien mit 16,1 Prozent (Wettquote 6,2), Frankreich mit 14.3 Prozent (Wettquote 7), England mit 11,4 Prozent (Wettquote 8,8), Spanien mit 11,1 Prozent (Wettquote 9) und Deutschland mit 8,3 Prozent (Wettquote 12). Die schlechtesten Gewinnaussichten haben Saudi Arabien und Costa Rica mit jeweils 0,1 Prozent (Wettquote 1000). ). Diese Wahrscheinlichkeitsvorhersagen können sich allerdings jederzeit ändern, wenn es relevante neue Informationen gibt. Wenn sich zum Beispiel Messi verletzen würde, würde das sofort alle Wettquoten und somit alle Wahrscheinlichkeitsvorhersagen ändern. Der Wettmarkt verarbeitet diese Informationen unglaublich schnell.
Der Autor
Christoph Kuzmics ist seit 2015 Professor für Mikroökonomik, sowie Mitglied des profilbildenden Bereichs Complexity of Life (COLIBRI), an der Universität Graz. Davor war Kuzmics Professor an der Universität Bielefeld, und von 2003 bis 2011 Assistenzprofessor an der Kellogg School of Management, Northwestern University.






